Die Satzgruppe des Pythagoras umfasst insgesamt drei Sätze. Diesen Sätzen gehören der Satz des Pythagoras, der Kathetensatz des Euklid sowie der Höhensatz des Euklid an.
Inhaltsverzeichnis
Der Satz des Pythagoras
Heute ist der Satz des Pythagoras ein wichtiger Teil moderner Geometrie. Deshalb sollten Schüler und Schülerinnen zuerst einmal wissen, wofür der Satz des Pythygoras überhaupt verwendet wird. Im Fokus steht ein Dreieck. Dem Satz des Pythagoras zufolge genügt es, die Länge von zwei Seiten zu kennen, um dadurch die Länge der dritten Seite zu ermitteln. Eine wichtige Voraussetzung ist jedoch, dass das Dreieck einen rechten Winkel haben muss. Nachfolgende Grafik zeigt ein Dreieck mit rechtem Winkel auf, an dem der Satz des Pythagoras angewendet werden kann.
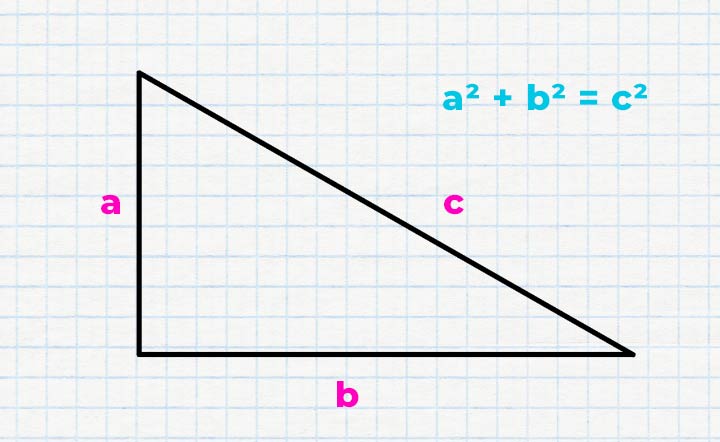
Bei dieser Grafik ist der rechte Winkel von 90 Grad in der unteren linken Ecke angeordnet. An den rechten Winkel grenzen die Seiten a und b, die als Katheten bezeichnet werden. Die längste Seite mit der Bezeichnung „c“ wird als Hypotenuse bezeichnet. Nachfolgende Gleichung wird in Verbindung mit dem Satz des Pythygoras am häufigsten genutzt.
a² + b² = c²
Rechenbeispiel 1: Berechne am folgenden Beispiel die Länge der Hypotenuse c.
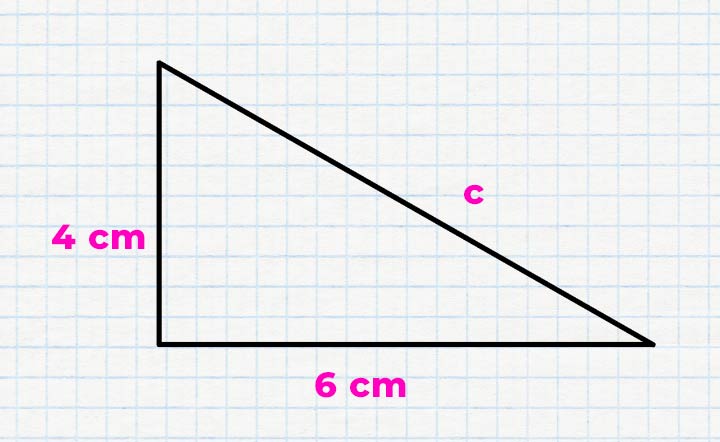
Die Katheten des Dreiecks sind 4 cm und 6 cm lang. Die Gleichung wird nach dem Satz des Pythagoras nach c umgestellt, indem diese beiden Angaben eingesetzt werden. Berechnen Sie die Quadrate und beachten Sie dabei, dass Zahlen und Einheiten quadriert werden müssen. Fassen Sie die Werte und ziehen Sie die Wurzel. Die Länge der Hypotenuse c beläuft sich auf 7,21 cm.
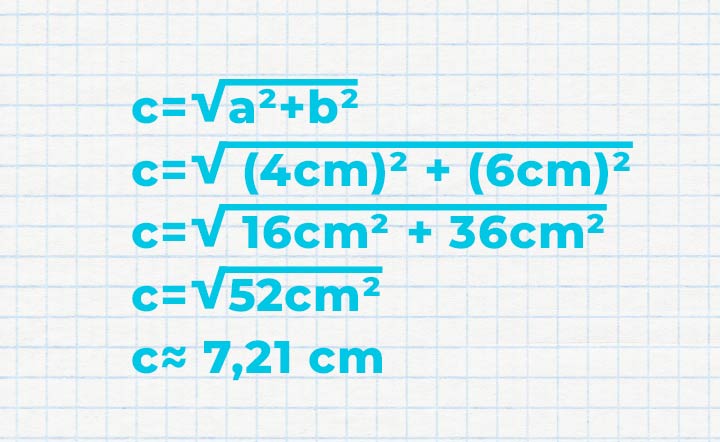
Der Höhensatz des Euklid
Der Satzgruppe des Pythagoras gehören ebenfalls der Höhensatz und Kathetensatz an. Der Höhensatz wird an einem rechtwinkligen Dreieck angewendet, der jedoch eine Höhe h aufweist.
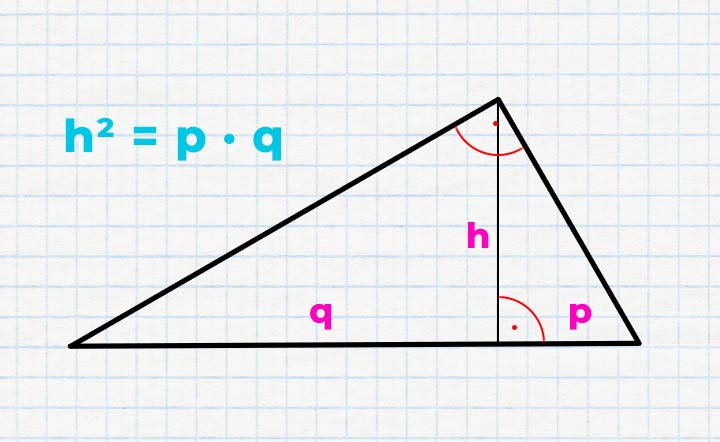
Die Formel für den Höhensatz bildet den Zusammenhang zwischen Höhe und Achsenabschnitten p und q.
h² = p x q
Diese Formel kann ebenfalls direkt nach h oder alternativ nach p oder q umgestellt werden.
Rechenbeispiel 2: Höhensatz
Die nachfolgende Grafik stellt ein Dach dar. Von der Spitze samt rechtem Winkel verläuft die Höhe h nach unten in Richtung Dachboden. Die beiden Längen auf dem Boden sind 4 und 6 m lang. Wie groß ist die Höhe h?
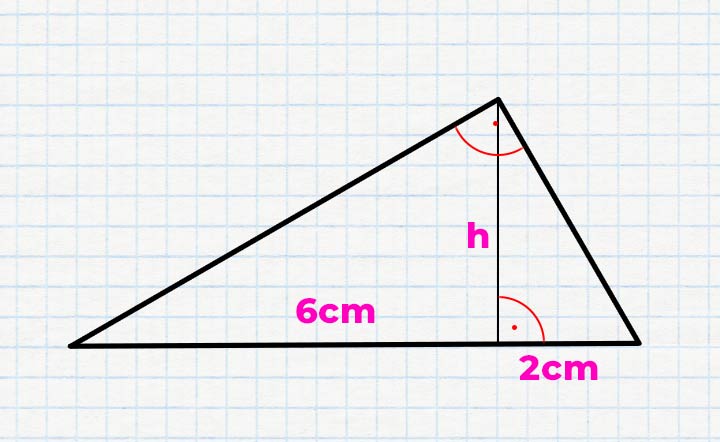
Lösungsansatz: Die beiden Angaben zeigen im direkten Vergleich zur Grafik auf, dass p = 2 m und q = 6 m ist. Um die Höhe h zu suchen, wird die Formel vom Höhensatz nach h umgestellt. In diese Formel werden die Angaben eingesetzt und die Höhe h berechnet.

Der Kathetensatz des Euklid
Der Kathetensatz des Euklid gehört ebenfalls der Satzgruppe des Pythagoras an. Beim Kathetensatz werden die Hypotenusenabschnitte als p und q bezeichnet. Generell gilt die Faustregel: Das Quadrat der Kathetenlänge ist von seiner Fläche so groß wie das Rechteck des zugehörigen Hypotenusenabschnitts sowie der kompletten Hypotenuse.
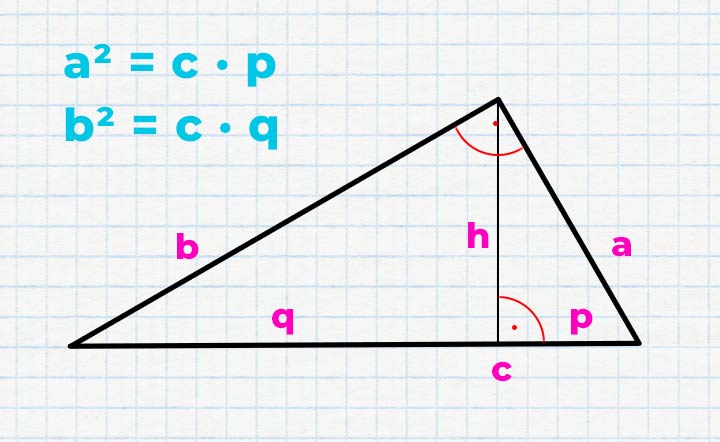
Die Gleichungen lauten wie folgt:
a² = c x p
b² = c x q





